# 蜀道山高校联合公益赛
搬运的 “我们中出了一个内鬼” 团队的 WP
# MISC
# Golf
全⻆字符绕过阻⽌名单
exec(input())
# Summit Potato
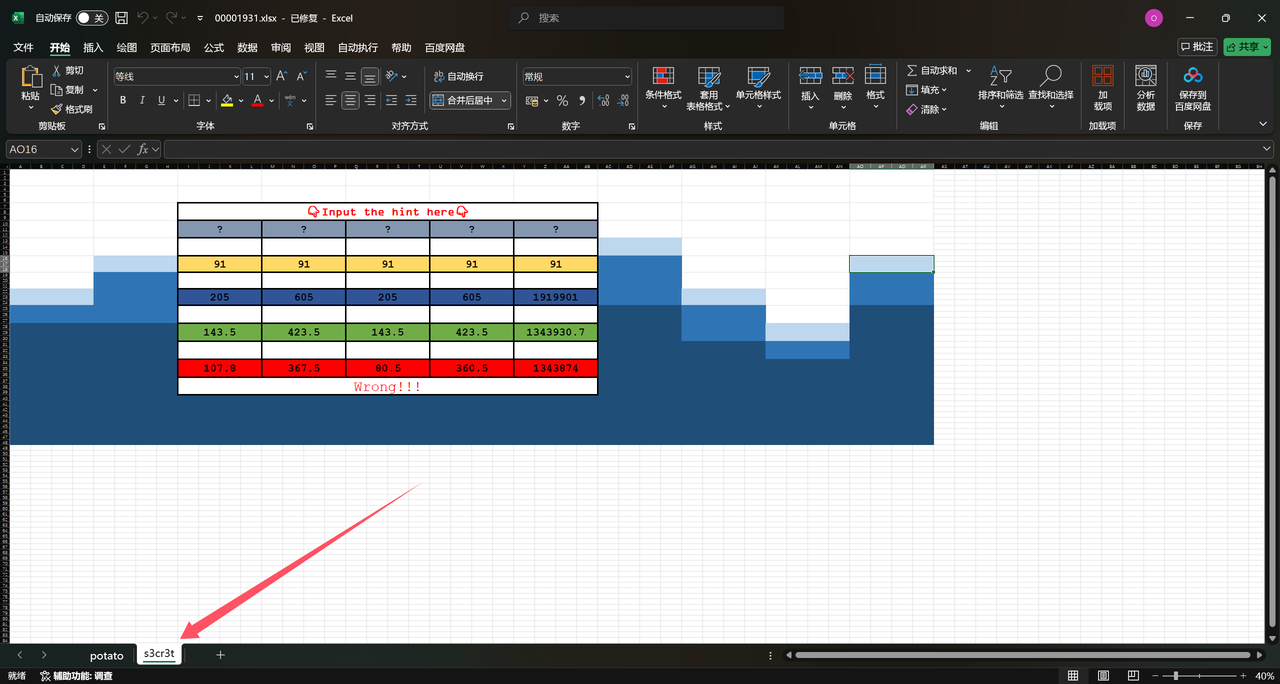
Potato.png 数据流后⾯分离出 xlsx ⽂件 (这里用 Foremost 出来 xlsx 文件,Binwalk 提取出来的打开有问题),第⼆个⼯作表按逻辑得到 Loe*n (第四个字符可以是任意字符),⽤来对 key.bin.xored 循环异或,根据语义和异或的规律尝试得到第四个字符为 n
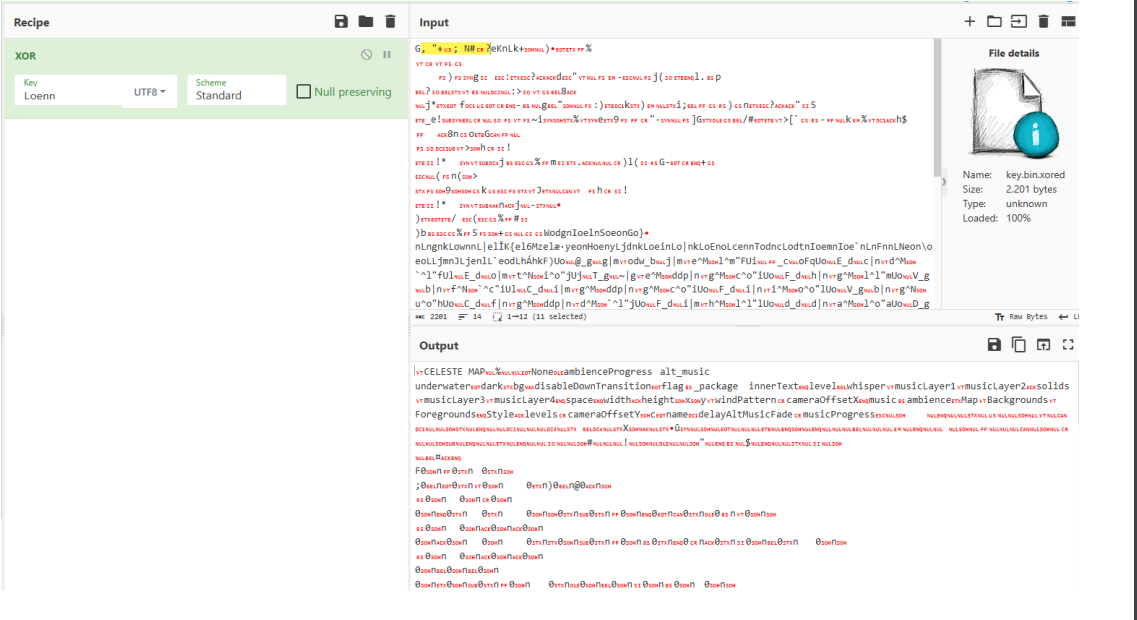
下载:https://github.com/CelestialCartographers/Loenn
相关问题:https://wiki.biligame.com/celeste/Loenn
再下⼀个蔚蓝,就可以打开 xor 后的地图
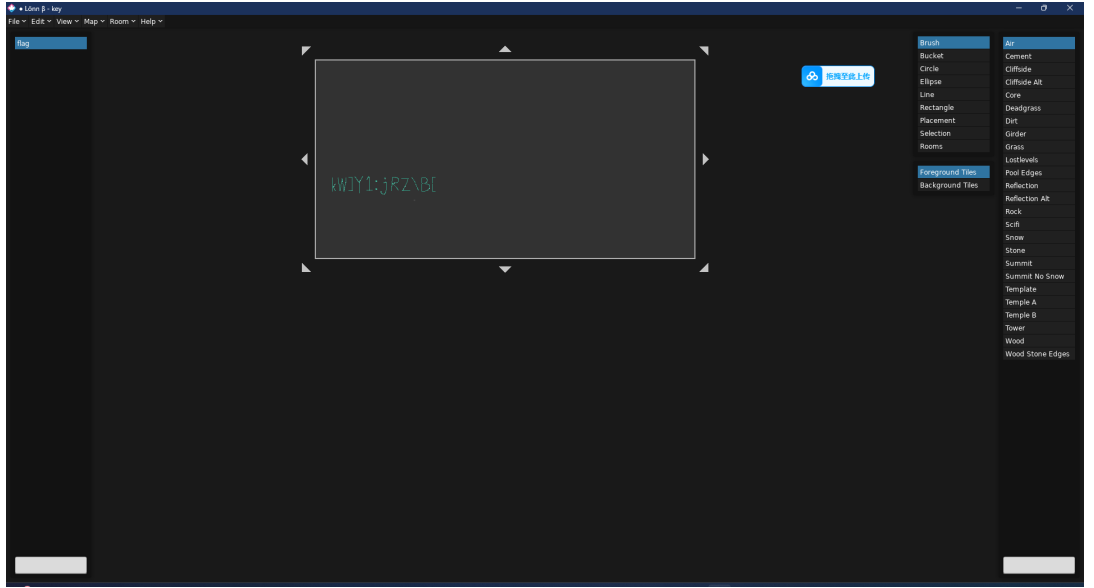
xlsx 解压后,在 media 有⼀个图⽚
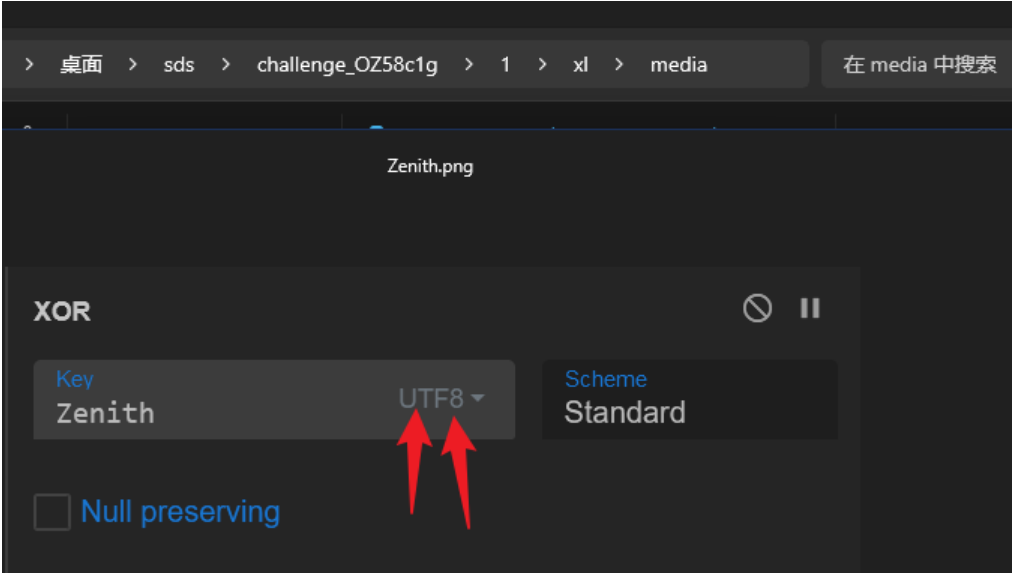
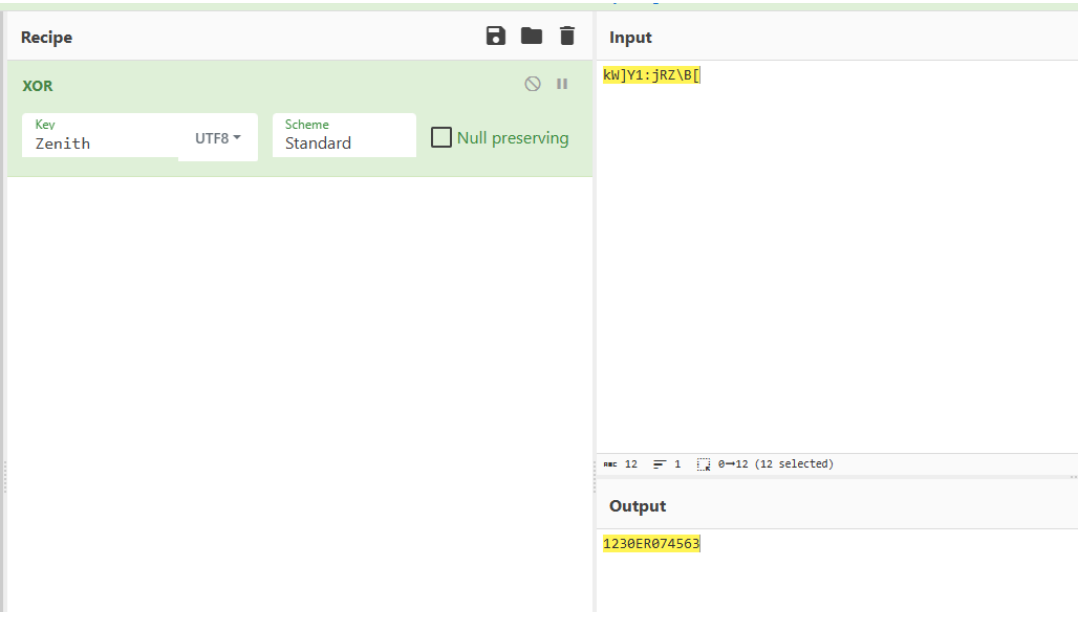
作为密码解开 flag.zip 压缩包
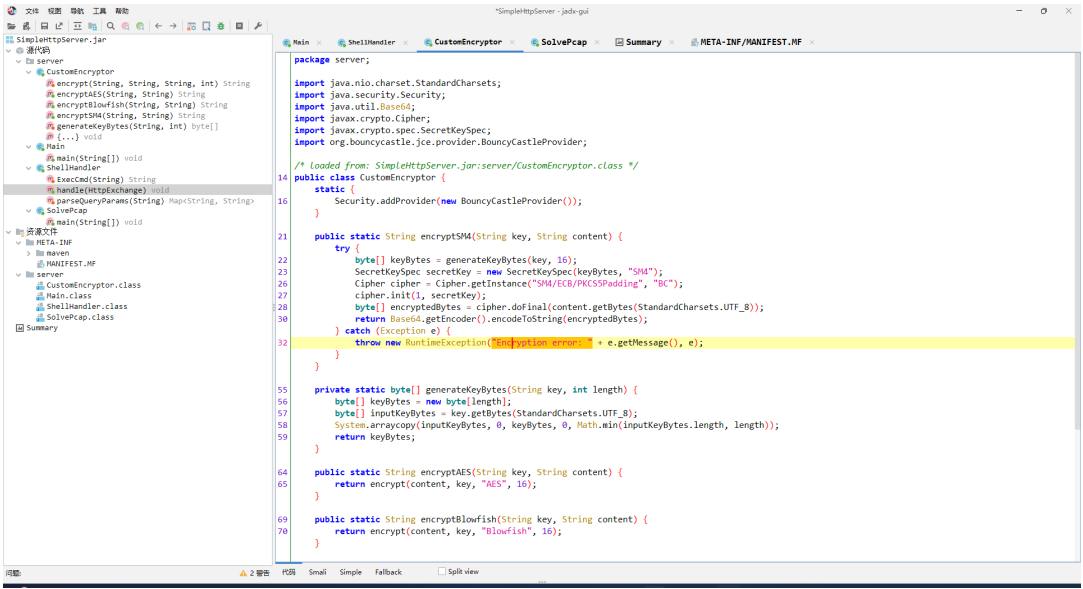
# javaPcap
cmd:base64
Method:给出,ECB
key->给出,顶真发现是bytes_to_long(cmd)(这⾥还在java的javax.crypto.spec.SecretKeySpec上卡了很久,觉得是类似于NodeJs的EVP_key,后来发现就是简单的补全截断
回显:明⽂->加密->base64->hex
基于逻辑进⾏解密
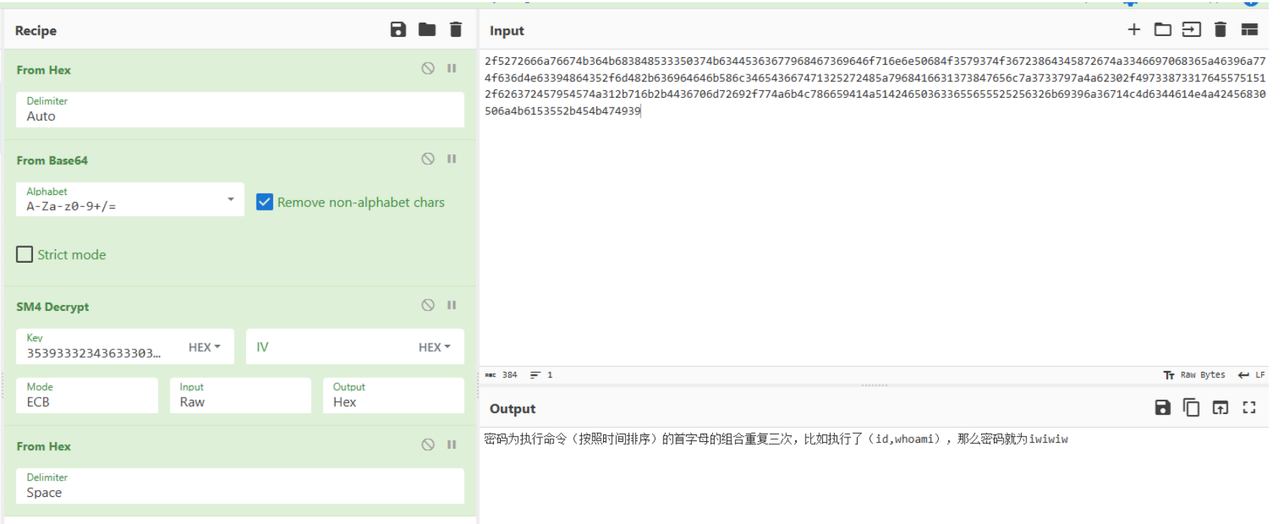
难泵且抽象的是 CybeyChef 这⾥解不出来,找个在线妙妙⼯具
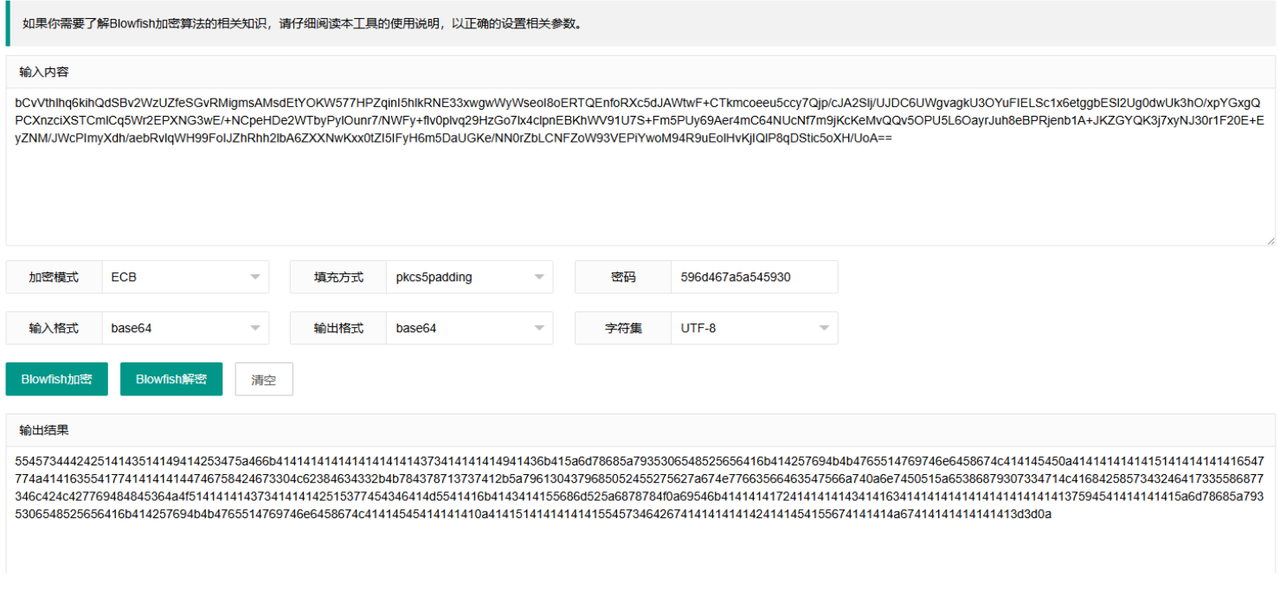
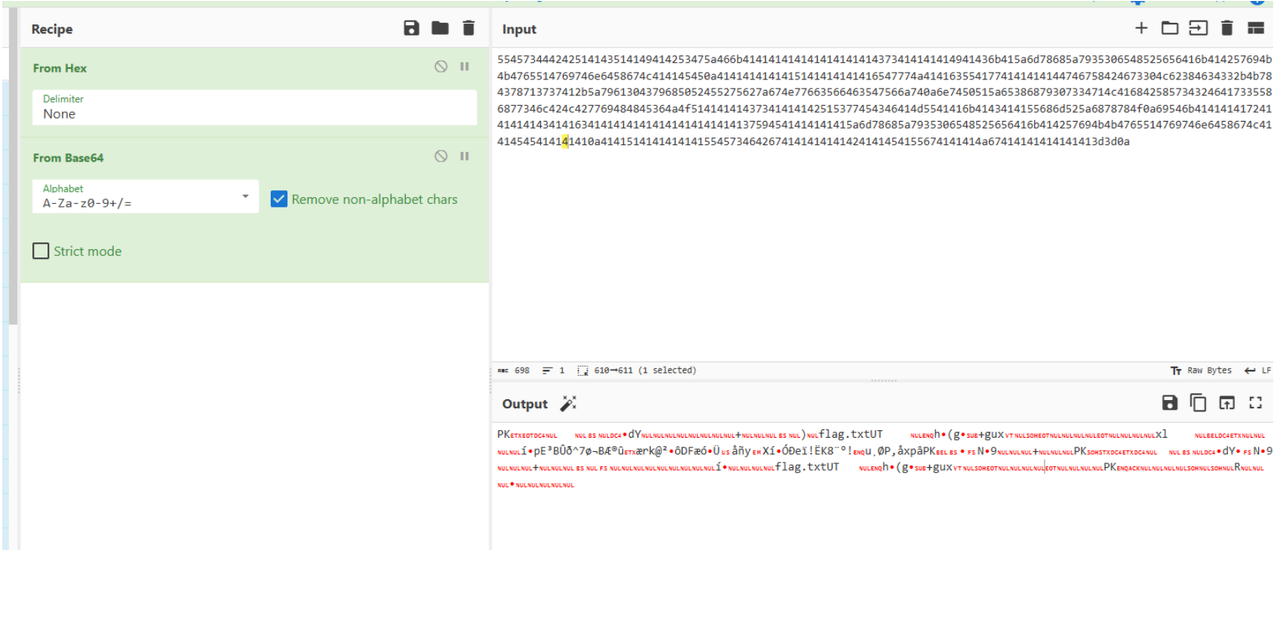
whoami
ls -alt
ls flag/
base64 flag/flag.zip
cat flag/hint.txt
# Reverse
# HelloHarmony
当成 zip 拆开,ets/modules.abc 丢进 abc-decompiler ,libs/arm64-v8a/libentry.so 丢进 IDA ArkTS 层业务逻辑中,导⼊ Emmm.Eeee 进⾏凯撒加密,构造函数传参为 5,导⼊ testNapi
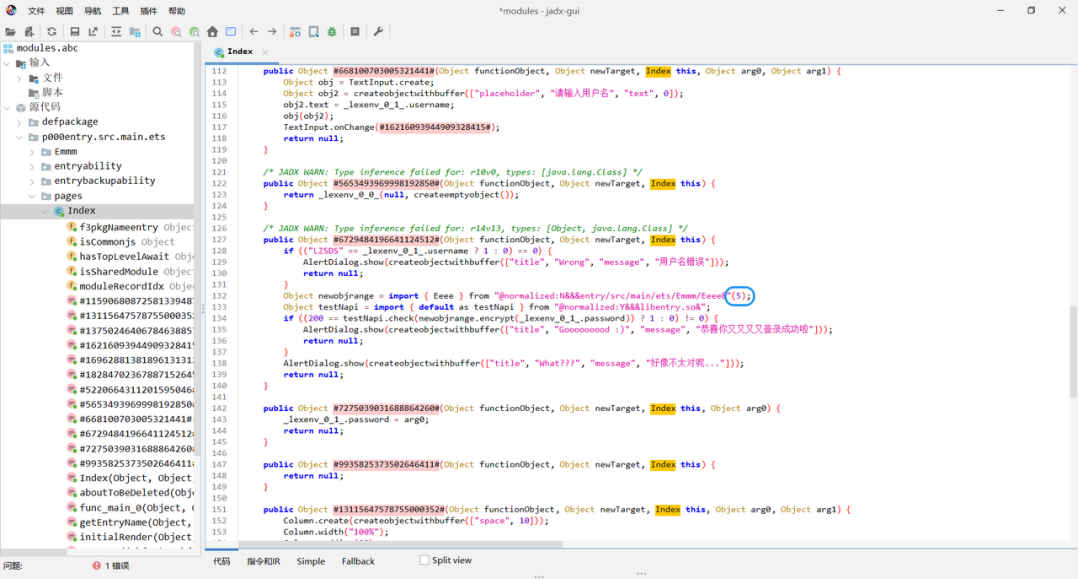
Native 层 sub_1F94 获得 UTF-8 字符串,从这⾥看起,进⾏了⼀系列算术运算,解密如下(IDA ⾥看到的 this 指向⼀个 256 字节的 box,this+256 指向派⽣的密钥)
#include <stdio.h>
#define u8 unsigned char
#define u32 unsigned int
u8 eeeee[] =
{
0xF6, 0xB0, 0xA6, 0x36, 0x9A, 0xB3, 0x2B, 0xBF, 0x94, 0x54,
0x15, 0x97, 0x93, 0x59, 0xBF, 0x50, 0x4D, 0xBF, 0x0A, 0x59,
0x06, 0xD7, 0x97, 0x50, 0xD6, 0x59, 0x54, 0xD7, 0xCF, 0x06,
0x5D, 0x20, 0x1D, 0x5A, 0x22, 0xEE, 0x99, 0x1F, 0xE1, 0x18,
};
int main() {
u8 box[256] = {};
// banana
for (int i = 0; i < 256; ++i)
box[i] = (167 * i + 173) % 256;
u32 dkey[8] = {};
const char *a2 = "HelloSDS";
const char a3 = 8;
// bananana
for (int i = 0; i < 8; ++i)
dkey[i] = (a2[(i + 1) % a3] << 16) | (a2[i % a3] << 24) | (a2[(i + 2)% a3] << 8) | a2[(i + 3) % a3];
for (int i = 7; i >= 0; i--) {
// blablabla
u8 c = eeeee[39];
for (int j = 39; j > 0; j--) {
eeeee[j] = eeeee[j - 1];
}
eeeee[0] = c;
// bla
for (int j = 0; j < 40; j++) {
for (int k = 0; k < 256; k++) {
if (box[k] == eeeee[j]) {
eeeee[j] = k;
break;
}
}
}
// blablablablabla
((u32*)eeeee)[0] ^= dkey[i];
((u32*)eeeee)[1] ^= dkey[i];
}
for (int i = 0; i < 40; i++) {
if ('A' <= eeeee[i] && eeeee[i] <= 'Z') {
eeeee[i] = (eeeee[i] - 'A' - 5 + 26) % 26 + 'A';
} else if ('a' <= eeeee[i] && eeeee[i] <= 'z') {
eeeee[i] = (eeeee[i] - 'a' - 7 + 26) % 26 + 'a';
}
printf("%c", eeeee[i]);
}
return 0;
}
}
// LZSDS{y0u_4r3_4_m4573r_0f_cryp706r4phy}
# Map_maze
⼀个⻓度为 15*15 的数组,数组的元素是 {⾃⼰是否为墙的枚举值、指向上、下、左、右的指针}(幽默)
把构造迷宫的代码⽚段复制出来,IDE 批量⽂本替换,把它变成 int 数组并打印出来
#include <stdio.h>
int maze[225] = {0};
int main() {
int *v4 = maze;
int *v5 = maze + 105;
for (int k = 1; k < 15; ++k)
v4[k] = 1;
for (int m = 9; m < 15; ++m)
v4[m + 15] = 1;
for (int n = 0; n < 2; ++n)
v4[n + 30] = 1;
for (int ii = 3; ii < 8; ++ii)
v4[ii + 30] = 1;
for (int jj = 9; jj < 15; ++jj)
v4[jj + 30] = 1;
for (int kk = 0; kk < 2; ++kk)
v4[kk + 45] = 1;
for (int mm = 3; mm < 8; ++mm)
v4[mm + 45] = 1;
for (int nn = 12; nn < 15; ++nn)
v4[nn + 45] = 1;
for (int i1 = 0; i1 < 2; ++i1)
v4[i1 + 60] = 1;
for (int i2 = 7; i2 < 10; ++i2)
v4[i2 + 60] = 0;
v4[67] = 1;
for (int i3 = 11; i3 < 15; ++i3)
v4[i3 + 60] = 1;
for (int i4 = 0; i4 < 2; ++i4)
v4[i4 + 75] = 1;
for (int i5 = 3; i5 < 6; ++i5)
v4[i5 + 75] = 1;
for (int i6 = 11; i6 < 15; ++i6)
v4[i6 + 75] = 1;
for (int i7 = 0; i7 < 2; ++i7)
v4[i7 + 90] = 1;
v4[92] = 0;
for (int i8 = 3; i8 < 6; ++i8)
v4[i8 + 90] = 1;
for (int i9 = 7; i9 < 10; ++i9)
v4[i9 + 90] = 1;
for (int i10 = 11; i10 < 15; ++i10)
v4[i10 + 90] = 1;
v5[0] = 1;
v5[1] = 0;
v5[2] = 0;
v5[3] = 1;
for (int i11 = 4; i11 < 6; ++i11)
v5[i11] = 1;
for (int i12 = 7; i12 < 10; ++i12)
v5[i12] = 1;
for (int i13 = 11; i13 < 15; ++i13)
v5[i13] = 1;
for (int i14 = 0; i14 < 2; ++i14)
v5[i14 + 15] = 1;
for (int i15 = 7; i15 < 10; ++i15)
v5[i15 + 15] = 1;
for (int i16 = 11; i16 < 15; ++i16)
v5[i16 + 15] = 1;
for (int i17 = 0; i17 < 6; ++i17)
v5[i17 + 30] = 1;
for (int i18 = 7; i18 < 10; ++i18)
v5[i18 + 30] = 1;
for (int i19 = 11; i19 < 15; ++i19)
v5[i19 + 30] = 1;
for (int i20 = 0; i20 < 6; ++i20)
v5[i20 + 45] = 1;
for (int i21 = 11; i21 < 15; ++i21)
v5[i21 + 45] = 1;
for (int i22 = 0; i22 < 9; ++i22)
v5[i22 + 60] = 1;
for (int i23 = 13; i23 < 15; ++i23)
v5[i23 + 60] = 1;
for (int i24 = 0; i24 < 9; ++i24)
v5[i24 + 75] = 1;
v5[84] = 0;
v5[85] = 1;
v5[86] = 1;
v5[87] = 0;
for (int i25 = 13; i25 < 15; ++i25)
v5[i25 + 75] = 1;
for (int i26 = 0; i26 < 9; ++i26)
v5[i26 + 90] = 1;
v5[99] = 0;
v5[100] = 1;
v5[101] = 1;
v5[102] = 0;
for (int i27 = 13; i27 < 15; ++i27)
v5[i27 + 90] = 1;
for (int i28 = 0; i28 < 12; ++i28)
v5[i28 + 105] = 1;
for (int i = 0; i < 15; ++i) {
for (int j = 0; j < 15; ++j) {
printf(maze[i * 15 + j] ? "X" : " ");
}
printf("\n");
}
return 0;
}
// LZSDS{1979869e0c4ef6c542e54ae5c48f63ec}
迷宫有多解但是正确 flag 只有⼀个(幽默)
# Potato Toolkit
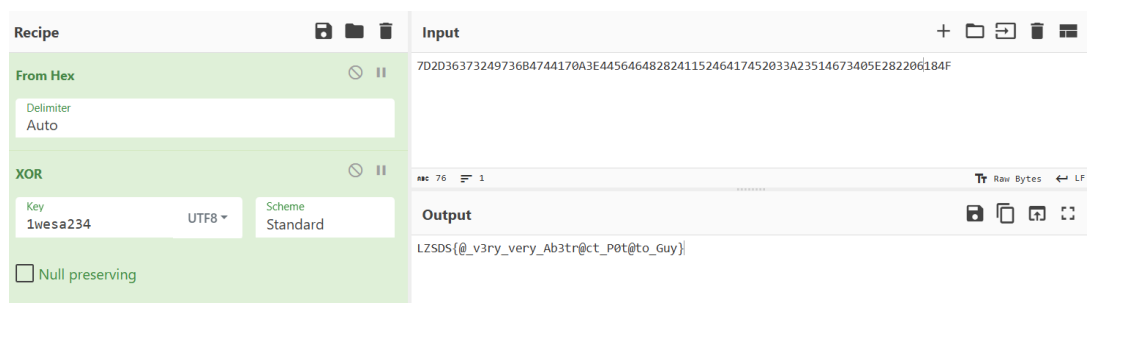
切到反汇编⾮图表视图,从头到尾快速粗略浏览⼀遍,找数据操作密集的位置就是主要逻辑,定位到 sub_1400012E0
开头判断了 a1 [6] 这个⽂本框为 1wesa234 ,后⾯读⼊ 38 字节并与这个⽂本框的⽂本循环异或(Aura 是真喜欢循环异或)
# 最⾼的⼭最⻓的河
随便找⼀个 EXE 补全最前⾯ 16 字节的 MZ 头
开始以为考的是异常处理,后来发现只是魔改 Base64 + TEA,有⼏处坑点
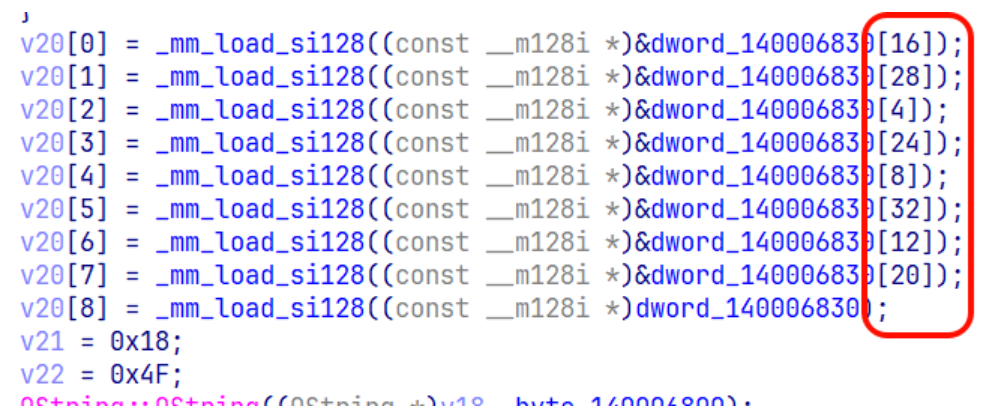
main 中调⽤的 sub_1400112CB (sub_14001D200) 为主要加密逻辑,sub_14001D200 较⼤的 for 循环为魔改 Base64,魔改点是先取三个字节的低 6 位,然后把三个字节⾼ 2 位拼接在⼀起
它下⾯调⽤的 sub_140011519 (sub_14001E3F0) 第⼀个 for 循环在把 Base64 字符(以 AbC1 为例)拼接成⼩端序 u32 时调换了中间的顺序,从低地址向⾼地址依次是 A C b 1
第⼆个 for 循环进⾏ TEA 加密,32 轮后还异或了⼀个常数
它下⾯调⽤的 sub_140011113 (sub_14001DF80) 在把 u32 数组拆成字节数组时,是按 u32 从最⾼字节向最低字节的顺序依次 append 的,相当于字节序转换
解密如下:
#include <stdio.h>
const int dword_140029DE0[5] = {0x4C, 0x5A, 0x53, 0x44, 0x53};
char enc[] = {165, 100, 159, 4, 57, 183, 166, 23, 34, 205, 38, 77, 125, 16,
130, 219, 133, 219, 39, 57, 66, 60, 30, 165, 34, 205, 38, 77, 125, 16, 130,
219, 214, 55, 104, 128, 177, 249, 21, 25, 68, 24, 66, 36, 143, 120, 162, 44};
void __fastcall sub_14001E1C0(unsigned int *a)
{
int v4; // [rsp+44h] [rbp+24h]
int i; // [rsp+64h] [rbp+44h]
unsigned int v9; // [rsp+1A8h] [rbp+188h]
unsigned int v10; // [rsp+1B0h] [rbp+190h]
v10 = dword_140029DE0[4] ^ a[1];
v9 = dword_140029DE0[4] ^ a[0];
v4 = -957401312 + 1640531527 * 32;
for (i = 0; i < 32; ++i)
{
v4 -= 1640531527;
v9 += (dword_140029DE0[1] + (v10 >> 5)) ^ (v4 + v10) ^
(dword_140029DE0[0] + 16 * v10);
v10 += (dword_140029DE0[3] + (v9 >> 5)) ^ (v4 + v9) ^
(dword_140029DE0[2] + 16 * v9);
}
a[1] = v10;
a[0] = v9;
}
const char *b64alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/";
int getIndex(char c)
{
for (int i = 0; i < 64; i++)
{
if (b64alphabet[i] == c)
{
return i;
}
}
return -1;
}
int main()
{
for (char *b = enc; b < enc + 48; b += 4)
{
char c = b[2];
b[2] = b[1];
b[1] = c;
c = b[3];
b[3] = b[0];
b[0] = c;
}
for (unsigned int *b = (unsigned int *)enc; b < (unsigned int *)(enc + 48); b += 2)
{
sub_14001E1C0(b);
}
for (char *b = enc; b < enc + 48; b += 4)
{
char c = b[2];
b[2] = b[1];
b[1] = c;
}
char flag[36];
int i = 0;
for (char *b = enc; b < enc + 48; b += 4)
{
char c1 = getIndex(b[0]);
char c2 = getIndex(b[1]);
char c3 = getIndex(b[2]);
char msbs = getIndex(b[3]);
flag[i++] = c1 | (msbs >> 4 << 6);
flag[i++] = c2 | (((msbs >> 2) & 3) << 6);
flag[i++] = c3 | ((msbs & 3) << 6);
}
printf("%s\n", flag);
return 0;
}
// // LZSDS{how_how_how_how_how_ow_ow_ow!}
# Crypto
# Something like coppersmith
dlp 问题,512bit 的 x 给了低 404bit,求解⾼位 108bit
查看 p-1 有⼏个⼩因⼦可以利⽤,bsgs+ph 求⼀下⾼位,拼起来就是完整的 x
from sage.all import *
p = 6302810904265501037924401786295397288170843149817176985522767895582968290551414928308932200691953758726228011793524154509586354502691822110981490737900239
g = 37
y = 1293150376161556844462084321627758417728307246932113125521569554783424543983527961886280946944216834324374477189528743754550041489359187752209421536046860
xl = 17986330879434951085449288256517884655391850545705434564933459034981508996937405053663301303792832616366656593647019909376
enc = b'\x08[\x94\xc1\xc2\xc3\xb9"C^\xd6P\xf9\x0c\xbb\r\r\xaf&\x94\x8cm\x02s\x87\x8b\x1c\xb3\x92\x81H\xe7\xc6\x190a\xca\x91j\xc0@(\xc5Fw\x95\r\xee'
# 512-404=108
a = pow(g, 2**404, p)
b = y*pow(g, -xl, p)
subs = [2, 385057, 727646221919, 193893885660581]
F = GF(p)
xhs = [discrete_log_lambda(F(pow(b, (p-1)//sub, p)), F(pow(a, (p-1)//sub, p)),(0, sub)) for sub in subs]
xh = crt(xhs, subs)
x = xh*2**404 + xl
print(f"{xh = }\n{x = }\n{pow(g, x, p) - y}")
xh = 75264534032313167327310698296002
x = 3109629341267338542281598485842430908207399697796047162247944601790472203194018819012768066635985627456532841488248491869575854365325351247411886736433408
from Crypto.Cipher import AES
import hashlib
key = hashlib.md5(str(x).encode()).digest()
aes = AES.new(key=key, mode=AES.MODE_ECB)
flag = aes.decrypt(enc)
print(flag)
# xorsa
hint1 和 hint2 异或得 p,phi 和 e 不互素,GCD ⼀下,求出 m^2,开⽅得到 flag
import gmpy2
from Crypto.Util.number import *
c = 13760578729891127041098229431259961120216468948795732373975536417751222443069805775693845560005881981622202089883866395577154701229046245882282127054969114210307175116574178428823043817041956207503299220721042136515863979655578210499512044917781566303947681251248645504273995402630701480590505840473412765662
n = 1424703821182138520975906725684623222744416317309919908525779037059045074966520655616336475426918225535808494835434582789898723475666213397463311706290237081185546666535178402712533311266307508539567650112175978669972014909857643314181737564928779420725539793335830274229206316999461309927000523188222801659
hint1 = 8938538619961731399716016665470564084986243880394928918482374295814509353382364651201249532111268951793354572124324033902502588541297713297622432670722730
hint2 = 1493298155243474837320092849325750387759519643879388609208314494000605554020636706320849032906759121914762492378489852575583260177546578935320977613050647
e = 2026
p = hint1^hint2
q = n // p
phi = (p - 1) * (q - 1)
k = GCD(e,phi)
print(k)
d = gmpy2.invert(e//k, phi)
m = pow(c, d, n)
flag = long_to_bytes(gmpy2.iroot(m,k)[0])
print(flag)
# LZSDS{fcfa4147-d982-4cd8-9ab7-50669e559736}